• Accueil
• Stages et concerts à venir
• Écouter le Dhrupad
• Vidéos de stages
• Qu'est ce que le Dhrupad?
• Qu'est ce qu'un Raga?
• Musique indienne
  contre occidentale
• Exemples réglage pur contre réglage occidental
• Biographie de Shivala
• Association Dhrupad
• Contact

MUSIQUE INDIENNE
CONTRE OCCIDENTALE

- English original by Ketil Helmersberg

Au cœur de la musique indienne est le raga, qui est un état d'esprit, un sentiment, exprimé par une gamme microtonale. Il existe de nombreux ragas, et chacun a sa propre ambiance et sa propre gamme microtonale correspondante basée sur ce qu'on appelle la série harmonique naturelle - la loi naturelle des vibrations.

Cependant, au cours des 100 dernières années, la musique indienne a été influencée par un système tonal étranger qui n'est pas basé sur la série harmonique naturelle. Le système tonal occidental a influencé la musique indienne principalement parce que des musiciens indiens ont adopté les instruments occidentaux à tons fixes. C'est surtout le cas de l'harmonium, qui est devenu très populaire et très répandu en Inde.

Le système tonal de la musique occidentale est basé sur une division artificielle de l'octave en douze intervalles égaux. Cela signifie tout d'abord que les notes sont désaccordées, mais aussi que le nombre d'intervalles disponibles pour l'expression musicale est très limité par rapport aux possibilités infinies de la série harmonique naturelle.

Par conséquent, il n'est pas possible de jouer un raga correctement avec un instrument à tons fixes basé sur le système tonal occidental. C'est comme essayer de faire une copie d'une peinture sans avoir accès aux couleurs de l'original. Ce système est incapable d'exprimer toutes les nuances subtiles des intervalles naturels utilisées dans un grand nombre de ragas.

Le système tonal occidental est cependant devenu si dominant dans le monde aujourd'hui, ainsi qu'en Inde, que les gammes microtonales originales des ragas sont en danger de disparition. De nombreux érudits de la musique indienne considèrent que ce développement est très préjudiciable, non seulement pour la musique indienne en tant qu'art, mais surtout parce que les ragas sont à l'origine un moyen de développement de la conscience.

En remplaçant les gammes microtonales originales par des approximations en gammes occidentales, la force et la puissance originelles des ragas sont en train de se perdre - ce qui n'est pas seulement une considération théorique, mais une constatation basée sur l'expérience. Pour cette raison, nous pensons qu'il est important de sensibiliser le public à ce problème. Nous donnons donc ici une description, une comparaison et un résumé historique des systèmes tonaux originaux indiens et occidentaux.

L'ESSENCE DE LA MUSIQUE

On peut dire que l'essence de la musique est la relation entre les sons. Le dictionnaire Oxford donne la définition suivante du mot «musique»

À la fois dans la musique occidentale et dans la musique indienne traditionnelle, les sons de la musique sont ordonnés en gammes. Ces gammes sont à la base de l'expression musicale. Le plus souvent, une gamme a 7 notes, bien qu'elle puisse en avoir moins ou plus. Une des notes de la gamme est appelée la note clé, la note de base de la gamme. Si nous comparons la gamme à une famille, la note clé est comme la mère, tandis que les autres notes sont comme les enfants. Parfois, les enfants jouent entre eux, mais ils jouent toujours avec la mère en arrière plan, et ils reviennent toujours vers la mère. Par conséquent, les relations les plus importantes entre les notes de la gamme sont entre chacune des notes et avec la note clé.

La note clé est la note de départ à partir de laquelle nous construisons une gamme musicale. Les différentes notes de la gamme sont souvent nommées par leur position à partir de la note clé. Par conséquent, la deuxième note de la gamme est appelée la seconde, la quatrième note la quarte, la cinquième note la quinte, et ainsi de suite.

INTERVALLES D'INTONATION JUSTE

Quand nous frappons la corde d'une guitare, elle produit un son. Le son est diffusé par la corde vibrante en faisant vibrer les molécules d'air adjacentes. La vibration se propage dans toutes les directions de l'espace comme des vagues à la surface d'un étang. Quand elle atteint les membranes de nos oreilles, elle les font vibrer, ces vibrations sont ensuite transformées en impulsions nerveuses que nous percevons comme un son continu d'une hauteur définie.

L'air vibre à la même vitesse que la corde, et la hauteur du son est déterminée par la vitesse de la vibration, qui est appelée la fréquence. La fréquence est mesurée en hertz (Hz), c'est le nombre de vibrations par secondes. La fréquence de la corde vibrante est déterminée par sa longueur, son épaisseur et sa tension.

En faisant abstraction des dispositifs d'amplification possibles, l'amplitude de la vibration détermine le volume. Alors que la fréquence, et donc la hauteur du son, reste la même tant que la corde vibre, l'amplitude diminue progressivement, ce qui fait que le son disparaît progressivement.

Quand nous écoutons le son d'une corde de guitare, nous n'entendons pas un seul son, mais de nombreux sons de hauteurs différentes. En fait, nous entendons un composé de sons. Nous entendons un son principal, le son de base, mais en plus nous entendons les harmoniques. Les intervalles, qui sont les différences de hauteur entre ces sons ne sont pas placés au hasard. Ils sont très précis et ordonnés.

Abstraction faite d'éventuelles limitations du milieu physique de la corde, les harmoniques sont des multiplications exactes de la fréquence du son fondamental. Si par exemple le son principal est de 200 Hz, la première harmonique, le deuxième son, sera de 400 Hz, soit deux fois la fréquence de base. La seconde harmonique, ou le troisième son, sera de 600 Hz, soit trois fois la fréquence de base. La troisième harmonique, ou le quatrième son, sera de 800 Hz, soit quatre fois la fréquence de base. La quatrième harmonique, ou le cinquième son, sera 1000 Hz, cinq fois la fréquence de base, et ainsi de suite. Nous pouvons illustrer cela en utilisant une échelle de fréquences en Hz:

Un son et ses harmoniques

Cette séquence de sons est appelée la série harmonique et représente une suite d'intervalles naturels. Ils expriment les intervalles sonores de la nature, aussi appelés intervalles d'intonation juste. Dans les cultures les plus importantes de l'histoire du monde, on a construit des gammes musicales basées sur ces intervalles. De même en Europe - tout au long du Moyen Age et de la Renaissance - le consensus était que les intervalles de l'intonation juste devraient être à la base de la musique.

Les intervalles de l'intonation juste peuvent être exprimés sous forme de fractions des numéros des sons de la série harmonique, qui sont égales à un nombre divisé par l'autre. Nous pouvons illustrer cela de la manière suivante :

Mathématiques de l'intonation juste

Le rapport de l'intervalle entre deux sons dans la série harmonique est le numéro du deuxième son divisée par le numéro du premier son. En multipliant le numéro du premier son par le rapport, on obtient le numéro du deuxième son. Ceci est montré dans l'exemple suivant:

Le premier intervalle que nous avons est du son 1 au son 2, qui dans ce cas est de 200 Hz à 400 Hz. Cet intervalle est également appelé une octave. Le rapport de cet intervalle est de 2/1. En multipliant 1 par le rapport d'intervalle, nous obtenons 2. De même, en multipliant 200 Hz par le rapport de l'intervalle on obtient 400 Hz, la fréquence du 2ème son.

Le deuxième intervalle que nous avons est du son 2 au son 3, qui dans ce cas est de 400 Hz à 600 Hz. Le rapport de cet intervalle est de 3/2. En multipliant 2 par le rapport d'intervalle, nous obtenons 3. De même, en multipliant 400 Hz par le rapport de l'intervalle on obtient 600 Hz, la fréquence du 3ème son.

Le troisième intervalle que nous avons est du son 3 au son 4, qui dans ce cas est de 600 Hz à 800 Hz. Le rapport de cet intervalle est de 4/3. En multipliant 3 par le rapport d'intervalle, nous obtenons 4. De même, en multipliant 600 Hz par le rapport de l'intervalle on obtient 800 Hz, la fréquence du 4ème son.

Mais nous avons aussi des intervalles comprenant plus d'un intervalle, comme par exemple du son 4 au son 7, qui dans ce cas est de 800 Hz à 1400 Hz. Le rapport de cet intervalle est de 7/4. En multipliant 4 par le rapport d'intervalle, nous obtenons 7. De même, en multipliant 800 Hz par le rapport de l'intervalle on obtient 1400 Hz, la fréquence du 7ème son, et ainsi de suite.

De la série harmonique, peuvent être trouvés des intervalles de toutes tailles et degrés. Un intervalle, ou la différence entre deux intervalles, peut être si petit qu'il est à peine perceptible pour une oreille non entraînée. Une telle différence infime est appelée un microton et les gammes basées sur le système tonal de la série harmonique sont donc appelées microtonales.

Nous pouvons aussi voir qu'il y a un principe mathématique sous-jacent. Tous les rapports d'intervalles dans la série d'harmoniques sont exprimées par des nombres entiers. Donc, ce qui caractérise les intervalles naturels, ou intervalles d'intonation juste, c'est qu'ils peuvent être exprimés en fractions de nombre entier. Ce fut aussi la découverte des Grecs, comme Pythagore, des Sumériens, des Indiens, des Chinois et de beaucoup d'autres cultures de l'histoire du monde, qui pensaient tous que les gammes musicales devraient être basées sur les ces intervalles.

Ainsi, on peut choisir une note clé et construire une gamme naturelle, ou gamme en intonation juste, en ajoutant des intervalles de fractions de nombres entiers. Le choix des intervalles pour créer une gamme est une véritable science. Dans la tradition indienne la sélection des intervalles de la gamme est telle que de jouer les notes crée une humeur ou un sentiment particulier, qui est appelé un raga. Un principe de base est que les intervalles de fractions de petits nombres sont plus harmonieux que ceux des grands nombres. A mesure que les nombres des fractions deviennent plus grandes, les intervalles deviennent moins harmonieux et plus dissonants.

En appliquant des fractions de nombres entiers, on peut établir une collection d'intervalles sur une octave, du plus petit au plus grand. Ces intervalles constituent alors une série de notes à partir de laquelle on peut sélectionner celles qui seront utilisées dans une gamme.

Dans la tradition européenne, on utilise depuis longtemps un système tonal à douze intervalles dans l'octave, constituant une série de notes appelées demi-tons. A partir de ces demi-tons on sélectionne ceux qui doivent être utilisés dans différentes gammes. A l'origine, ces douze notes de la musique occidentale étaient en conformité avec l'intonation juste.

À titre d'exemple, nous pouvons choisir de donner la préférence aux intervalles les plus harmonieux, qui sont constitués des fractions de plus petits nombres, et monter une collection de douze notes à peu près également réparties dans une octave. Ainsi, nous aurons une série de demi-tons en intonation juste. Nous pouvons commencer avec le A standard de la musique occidentale, qui a la fréquence de 440 Hz.

Exemple d'une série de notes en intonation juste

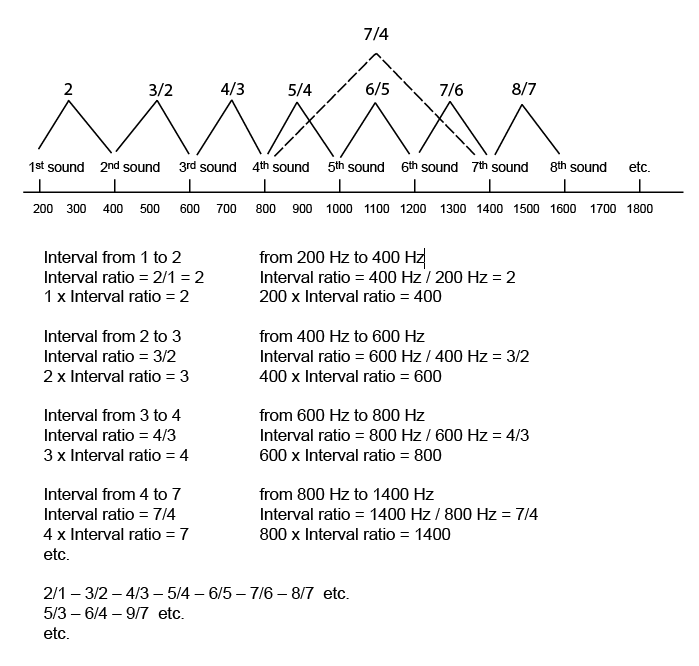
Comme on le voit dans le tableau, on peut aussi calculer les rapports d'intervalles entre les demi-tons. Pour ce faire, on prend le rapport d'intervalle d'une note - calculée à partir de la note clé - et on soustrait le rapport d'intervalle de la note précédente - également calculée à partir de la note clé. Ceci est réalisé en multipliant un rapport d'intervalle par l'inverse du rapport d'intervalle à soustraire. Par exemple, pour trouver le rapport d'intervalle de A# à B, on soustrait le rapport d'intervalle 16/15 du rapport d'intervalle 9/8, ce qui est fait par la multiplication suivante : 9/8 x 15/16 = 135/128.

On peut également ajouter des rapports d'intervalle. Pour ce faire, on multiplie une fraction par l'autre. Par exemple, pour ajouter la fraction 16/15, qui est la moitié de la note de A à A#, à la fraction 135/128, qui est la moitié de la note de A# à , on fait le calcul suivant: 16/15 x 135/128 = 9/8.

De cette série de douze notes, on utilise principalement 7 notes pour une gamme musicale - qui devrait normalement être une séquence de tons entiers et de demi-tons. Cependant, quand mous calculons les rapports d'intervalle entre les demi-tons de la série de douze notes, nous constatons qu'ils ne sont pas égaux. Alors que le rapport de A à A# est de 16/15, le rapport de A# à B est 135/128 etc. Cela signifie que si l'on veut utiliser une autre note de A comme note principale, la séquence des intervalles ne serait pas la même. En pratique, cela signifie que pour appliquer l'intonation juste à un instrument à tons fixes, comme un orgue ou un piano, on doit accorder l'instrument en fonction de la note de clé choisie. Si l'on veut changer la note clé, ce qui signifie commencer la même gamme d'une autre note, à une autre hauteur, il est probable qu'on doive raccorder l'instrument tout entier.

C'est le problème pratique auquel à été confrontée la musique occidentale quand les musiciens ont commencé à utiliser des instruments à tons fixes, parce qu'ils voulaient être en mesure de changer fréquemment de notes clés, même au milieu d'une composition. Nous pouvons illustrer ce problème par l'exemple suivant:

La série de douze notes ci-dessus est basée sur la note clé A. Donc, si nous l'utilisons pour faire une gamme de A majeur, nous verrons ce qui se passe si nous essayons par exemple de changer la note clé à C. La gamme de A majeur est constituée des notes A - B - C# - D - E - F# - G#, tandis que la gamme de C majeur est constituée des notes C - D - E - F - G - A - B.

Une gamme en A majeur en intonation juste transposée en gamme de C majeur

Nous voyons que dans de nombreux cas, les intervalles entre les notes des deux gammes sont différentes. Par exemple, l'intervalle entre la première et le deuxième note de la gamme de A majeur, de A à B, est de 9/8, tandis que l'intervalle entre la première et la deuxième note de la gamme de C, de C à D, est de 10/9. Le rapport de l'intervalle entre la deuxième et la troisième note de la gamme de A majeur est de 10/9, tandis que le rapport de l'intervalle entre la deuxième et la troisième note de la gamme de C est de 135/128, et ainsi de suite. Parce que dans de nombreux cas les intervalles entre les notes de ces deux gammes sont différents, ce sont en fait deux gammes différentes. Il n'est donc pas possible de changer la note clé de la gamme majeure A à C avec cette séquence d'intervalles.

LE SYSTÈME DE DOUZE TONS À TEMPÉRAMENTS ÉGAUX

En raison des problèmes liés à l'accordage en intonation juste, on a commencé en Europe, pendant la Renaissance, à expérimenter différents types "d'accords tempérés", qui modifient les intervalles de l'intonation juste de manière à pouvoir changer la note clé d'une gamme sans avoir à réaccorder. De nombreux systèmes différents d'accords tempérés ont été proposées au fil des ans, mais finalement, en 1850, le système le plus simpliste et radical, appelé le tempérament égal dodécaphonisme, est devenu la norme et l'est resté depuis dans la musique occidentale.

Le tempérament égal revient à égaliser les rapports d'intervalle entre les douze notes de l'octave et fixer les fréquences des notes. La fréquence de la note A au milieu du clavier du piano est par exemple fixée à 440 Hz. Nous pouvons donc commencer à partir de cette fréquence pour calculer le rapport d'intervalle de tempérament égal entre les demi-tons :

Les 440 Hz du A sont multipliés par le rapport de fréquence pour obtenir la fréquence du demi-ton suivant. Ensuite, cette nouvelle fréquence est multipliée par la même fraction pour obtenir le demi-ton suivant, et ainsi de suite. Cette opération est répétée 12 fois pour atteindre l'octave du A, Le A suivant sur le clavier d'un piano, dont la fréquence est le double de celle du A précédant.

Dans cette formule, on peut remplacer 440 Hz par 1 et l'octave par 2. On peut alors calculer que le rapport d'intervalle est de 1,0594630943593. Il s'agit d'un nombre irrationnel, ce qui signifie qu'il ne peut pas être converti en une fraction de nombre entier, ce qui signifie encore une fois que ce n'est pas un rapport d'intervalle en accord avec les harmoniques naturelles.

Donc, pour clarifier ce point; les 440 Hz de la note de A, sont multipliés par le rapport 1,05946 pour obtenir la fréquence du demi-ton suivant, qui est 466,1624 Hz, la note A#. Cette dernière fréquence est multipliée par le même rapport, 1,05946, pour obtenir la fréquence du demi-ton suivant, qui est 493,8824 Hz, la note B, et ainsi de suite. Lorsque cela est fait 12 fois, on arrive à l'octave, qui est le double de la fréquence de la note de départ. C'est le système de tempérament égal.

Ce système tonal est une solution de compromis, où l'on compromet l'harmonie, ou l'harmonie, les intervalles avec la possibilité de jouer une échelle dans n'importe quelle tonalité sans une échelle sonnant plus dissonant que l'autre. Cependant, cela signifie également qu'aucun des intervalles, sauf l'octave sont en conformité avec les harmoniques naturelles de l'intonation juste. Pour faire une comparaison entre ces deux systèmes tonaux, nous pouvons créer un tableau qui montre les douze tons précédents dans l'intonation juste avec les douze sons correspondants dans le tempérament égal:

Les douze tons en tempérament égal
comparés aux douze tons de l'intonation juste

Comme le montre ce tableau, les différences de fréquence entre le tempérament égal et l'intonation juste peuvent sembler peu nombreuses. Les partisans du système de 12 tons à tempérament égal seront diront probablement que cette différence n'est pas d'une grande importance. Ils pourraient aussi se demander pourquoi les intervalles de l'intonation juste seraient préférable, même s'ils peuvent être considérés comme naturels, ce qui signifie en accord avec les harmoniques naturelles.

Pour répondre à cette question, nous allons d'abord étudier les limites du système de douze notes à tempérament égal, puis son influence sur l'esprit de l'auditeur par rapport à l'intonation juste.

LIMITES DU SYSTÈME À TEMPÉRAMENT ÉGAL

Le système de tempérament égal à 12 tons a de grandes limitations pour l'expression musicale. Alors que dans l'intonation juste, on a un nombre infini d'intervalles naturelles disponibles, on a dans la gamme tempérée seulement 12 intervalles fixes.

Pour illustrer cette limitation, une grande partie de la musique populaire du monde et la musique contemporaine n'aurait pas existé dans la forme que nous connaissons si on avait dû se contenter des gammes tempérées. Cela concerne les genres de musique comme la musique irlandaise et le folk anglais, le Negro Spirituals, le Blues, le Soul, de nombreux types de jazz et le rock and roll. La raison en est que ces styles de musique s'appuient fortement sur des intervalles qui ne sont pas disponibles dans le système tempéré, même de manière approximative. Par exemple les notes dites bleues, qui sont souvent des tierces, quintes ou septièmes abaissés d'une gamme, mais pas suffisamment abaissés pour atteindre le demi-ton suivant de la gamme tempérée. Ces notes particulières sont à bien des égards le sang vital de ces styles musicaux. Sans eux, ils perdraient leur vitalité et leur pouvoir d'enchantement.

Il est possible de créer une sorte d'illusion d'une note bleue par exemple au piano en jouant des intervalles des demi-tons très rapidement, et ainsi créer un sentiment d'une note bleue, qui se situe quelque part entre deux demi-tons. Par conséquent, certains pianistes peuvent dans une certaine mesure compenser les limites du système tempéré par leur capacité technique. Mais ce n'est certainement pas la même chose que de jouer la note bleue elle-même, qui n'est pas disponible sur un piano à tempérament égal.

Les limites du système tempéré sont encore plus évidentes quand il s'agit de la musique indienne. Il existe environ 150 gammes microtonales ou ragas, en Inde aujourd'hui, et elles utilisent un bien plus grand nombre d'intervalles que les douze de la gamme tempérée.

En ce qui concerne les instruments à tons fixes, il y a aussi une autre limite : Une caractéristique importante pour exprimer un raga est de glisser entre les notes de la gamme. Ce n'est pas possible sur un instrument à tons fixes comme un piano ou un orgue, ce qui les rend donc moins appropriés pour jouer de la musique classique indienne comme instrument solo, même s'ils pouvaient être accordés correctement.

En outre, une limitation du tempérament égal est aussi que chaque note est fixée à une certaine fréquence. Dans la musique indienne traditionnelle ceci n'a jamais été fait. Chaque fréquence du son a une influence particulière, une qualité particulière ou un sentiment qui lui est propre. S'il n'y avaient pas des sentiments différents connectés à différentes fréquences sonores, il n'y aurait, par exemple, aucun intérêt à jouer dans différentes clés. Par la fixité des fréquences des notes, les douze tons égaux excluent de nombreuses fréquences. Ces fréquences sont comme effacée de la palette de la nature. Si nous comparons les fréquences sonores à la gamme des couleurs, c'est comme si les peintres ne disposaient que d'un nombre très limité de couleurs définies avec lesquelles travailler.

Un autre facteur très important en ce qui concerne les intervalles des sons est la façon dont ils affectent l'esprit. Dans les textes classiques de la musique indienne, ainsi que dans la philosophie grecque de Pythagore et de Platon, un facteur clé pour que la musique ait un effet positif est qu'elle doit plaire à l'esprit. Des études montrent que lorsque les gens entendent des intervalles d'intonation juste, ils les trouvent plus agréable, plus beaux que les intervalles équivalents en tempérament égal. Les gens sont en fait souvent étonnés que les intervalles de tempérament égaux puissent même être considérés comme harmonieux, lorsqu'ils les écoutent après avoir entendu des intervalles équivalents en intonation juste.

Des raisons esthétiques étaient aussi le principal argument contre le tempérament égal quand il a été introduit en Europe. Les théoriciens de la musique de l'époque estimaient que le tempérament égal dégradait la pureté tous les accords et l'attrait esthétique de la musique.

Il est également intéressant de noter qu'aucun des compositeurs occidentaux de renom ait écrit pour le tempérament égal, y compris Bach, Mozart, Beethoven, Schubert, Schumann, Chopin, Liszt, Wagner, Brahms et Tchaïkovsky. Mozart est même cité pour avoir dit qu'il tuerait quiconque jouerait sa musique en tempérament égal.

Toutefois, étant donné que les différences de fréquence entre les notes en tempérament égal et les notes équivalentes en intonation juste ne sont pas très grandes en termes de pourcentages, pourquoi y aurait-il une telle différence dans le niveau de plaisir à entendre leurs intervalles ? Est-ce que c'est seulement une question d'imagination ? Ou une sorte d'effet placebo?

La réponse à cette question est que les intervalles d'intonation juste sont plus consonants, ou harmonieux, que les intervalles équivalents en tempérament égal, ce qui peut être mis évidence par des expériences scientifiques modernes.

La consonance est un mot dérivé du latin : com, "avec" + sonare, + "son". Si l'on cherche sur le Wikipedia, elle est définie comme suit :

La dissonance est aussi un mot dérivé du latin : dis, «à part» + sonare, pour «sonner». Elle est définie par le musicologue moderne Roger Kamien de la façon suivante:

Consonance et dissonance sont toutes deux importantes pour l'expression musicale, mais les intervalles consonants doivent être vraiment consonants. Pour montrer par des expériences scientifiques modernes que les intervalles de l'intonation juste sont plus consonants que les intervalles équivalents dans le tempérament égal, il faut aller dans une branche de la physique appelée acoustique. Il s'agit d'une science complète en elle-même, parce que de nombreuses caractéristiques sont impliquées dans la relation entre les sons. Nous allons donc seulement regarder ce qui est considéré comme le facteur le plus important pour la consonance et la dissonance, qui est un phénomène appelé "battement".

BATTEMENT

Lorsque la différence de fréquence entre deux sons est supérieure à zéro Hz et inférieure à 20 Hz, nous les percevons comme un son. La fréquence du son combiné que nous entendons, sera la moyenne des deux sons. Le volume du son combiné, cependant, pour certaines raisons varie constamment, et c'est ce que l'on appelle le battement. C'est un phénomène qui est considéré comme la principale cause de dissonance. Le battement se produit en raison du changement continu de la relation entre les vibrations des deux sons.

Quand nous frappons la corde d'une guitare, les molécules d'air qui l'entoure commence à vibrer d'avant en arrière. La vibration se propage dans toutes les directions de l'espace. Le volume du son est le résultat de l'amplitude de la vibration.

Lorsque la fréquence de deux sons sont si proches qu'elles sont perçues comme un seul son, l'amplitude du signal combiné est la somme des amplitudes des deux sons. Comme l'un des deux sons vibre légèrement plus vite que l'autre, la relation entre leurs vibrations varie continuellement. À un moment donné, ils seront synchrone, ce qui signifie qu'ils vont osciller simultanément et la somme de leurs amplitudes sera au maximum. Ensuite, ils seront progressivement moins synchrone, ce qui signifie aussi que la somme des amplitudes sera progressivement moindre, jusqu'à ce qu'ils atteignent un point où ils vibrent en opposition l'un de l'autre. Si elles ont alors la même amplitude, la somme de leurs amplitudes sera nulle, ne produisant aucun son. Si l'amplitude de l'un des deux sons est plus grande que l'autre, l'amplitude du signal combiné ne sera pas à zéro, mais inférieur au son qui a la plus grande amplitude. Puis, progressivement, les vibrations des deux sons se redeviendront synchrone, ce qui signifie également que l'amplitude du son combiné va progressivement augmenter jusqu'à ce qu'ils atteignent leur maximum à nouveau, et ainsi de suite.

Le son que l'on entend est le résultat des deux sons qui frappent contre les membranes de notre oreille. Quand leurs vibrations sont synchrones, ils poussent et tirent les membranes de l'oreille simultanément, et donc avec une force combinée plus forte que l'un d'eux seul. Puis, quand leurs vibrations sont opposées, un son repoussera les membranes, tandis que l'autre va tirer, et donc ils vont plus ou moins se bloquer l'un l'autre, ce qui nous fait percevoir un bruit réduit, ou pas de son du tout. C'est ce qu'on appelle le battement. Cela peut être comparé à l'écoute de la radio en tournant le volume rapidement de haut en bas. La fréquence des battements est la différence de fréquence entre les deux sons. Nous pouvons illustrer ce phénomène par la figure ci-dessous, qui montre les vibrations sonores comme des vagues :

Exemple de battement

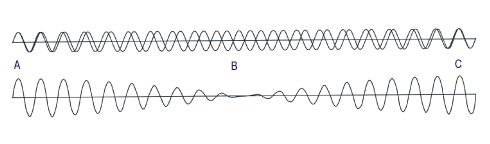
Les deux ondes du haut représentent les sons, l'onde du bas représente le son combiné que nous entendons. Les deux sons ont la même amplitude. L'amplitude variable de l'onde du bas montre la variation de volume du son combiné. Au point A, les deux sons sont plus ou moins synchrones, et l'amplitude combinée est à son maximum. Ensuite, ils deviennent moins synchrones et l'amplitude combinée diminue. Au point B, ils vibrent en opposition l'un à l'autre et l'amplitude combinée devient nulle, ne produisant aucun son. Puis, ils se synchronisent de nouveau progressivement, tandis que l'amplitude combinée augmente progressivement et atteint son maximum lorsque les deux ondes redeviennent synchrones, et ainsi de suite.

Lorsque la différence de fréquence augmente entre deux sons, tout en étant inférieure à environ 20 Hz, la fréquence du battement augmente. Lorsque la différence entre les sons devient supérieure à environ 20 Hz, le battement est remplacé par une expérience de rudesse. Lorsque la différence atteint un point quelque part entre un ton entier et une tierce mineure, le battement s'arrête et on entend deux sons distincts.

Le phénomène de battement montre qu'une légère variation de la fréquence a un fort impact sur le degré de consonance ou de dissonance. Nous pouvons illustrer cela par l'intervalle d'une octave désaccordé :

Exemple de battement pour une octave légèrement désaccordée

Nous voyons que, entre la note clé et l'octave pure, les harmoniques coïncident les unes avec les autres à différents niveaux, ce qui signifie qu'il n'y a pas de battement et donc que les deux sons ont un haut degré de consonance. Si nous désaccordons l'octave de 2 Hz, on obtient un battement entre les harmoniques à plusieurs niveaux, entre le 2ème et le 1er son, entre le 4ème et le 2ème son, entre le 6ème et le 3ème son, etc. Cela se traduira par une consonance réduite, ou une augmentation de la dissonance.

Nous pouvons maintenant comparer la consonance de l'intonation juste avec celle du tempérament égal en utilisant une quinte pure comme exemple. La quinte de 3/2 est considérée comme un intervalle hautement consonant.

Consonance comparée d'une quinte pure
en intonation juste et en tempérament égal

La quinte tempérée est en fait à 659.2564 Hz.

Nous voyons dans ce tableau qu'il y a un haut degré de coïncidence entre les harmoniques de la note clé et la quinte en intonation juste. Entre aucun de ces sons existe une différence apte à produire le battement.

Mais si nous regardons la quinte tempérée, aucune harmonique coïncide avec les harmoniques de la note clé, et nous obtenons un battement entre plusieurs des harmoniques. Le battement se produit entre le 3ème et le 2ème son, entre le 6ème et le 4ème son, entre le 9ème et le 6ème son, etc. Cela signifie que la consonance est beaucoup plus faible, ou la dissonance beaucoup plus forte, par rapport à l'intervalle équivalent en intonation juste.

INTONATION JUSTE COMBINÉE AU TEMPÉRAMENT ÉGAL

Pourtant, quelqu'un pourrait affirmer que même si un instrument à tons fixes, comme le piano ou l'orgue, accordé en tempérament égal, a ses limites, et que leurs intervalles sont moins agréables, pourquoi ne pourrait-il pas être utiliser pour l'accompagnement des chanteurs ou des musiciens en intonation juste ?

Pour répondre à cette question, considérons d'abord le chant en lui-même. Dans la tradition de la musique classique indienne, on apprend chanter à l'oreille en intonation juste. Les études montrent également que les chanteurs en général, qu'ils chantent seuls ou dans un groupe vocal, ont naturellement tendance à chanter en intonation juste lorsqu'ils ne sont pas accompagnés par un instrument à tempérament égal et tons fixes. Mais qu'advient-il si nous essayons de chanter en intonation juste accompagné d'un instrument accordé en tempérament égal ? Disons par exemple que nous chantons en gamme de LA majeur sur la base des intervalles d'intonation juste ci-dessus. Et disons que nous chantons une quinte pure, qui dans ce cas est la note MI, tandis qu'un accord de LA majeur est joué sur l'instrument, qui a les notes LA - DO# - MI. Voyons dans le tableau ci-dessous comment cela va fonctionner:

La quinte tempérée est en fait à 659.2564 Hz.

Le piano ou l'harmonium joueront la note clé et la quinte tempérée, qui sont les notes LA et MI, alors que le chanteur va essayer de chanter la note MI en intonation juste. Si nous examinons la différence de fréquence entre ces deux notes MI, nous voyons que non seulement leurs sons ne coïncident pas, mais que nous allons avoir du battement à tous les niveaux, à la fois entre les sons de base et à toutes les harmoniques les plus proches. Cela va sans doute créer un très fort degré de dissonance, qui va très probablement forcer le chanteur à chanter en tempérament égal. Ainsi, chanter en intonation juste en étant accompagné par exemple par un harmonium en tempérament égal ne sera probablement pas possible.

Ce que ces exemples tirés de la science de l'acoustique montrent, c'est que des modifications infimes des intervalles naturels, qui, pris isolément peuvent paraître comme des détails, peuvent provoquer de graves distorsions à plusieurs niveaux.

CONCLUSION

Pour conclure. La musicologie occidentale a dégradé l'harmonie et la beauté des intervalles sonores de la musique en déformant leurs rapports naturels. En outre, elle a construit une prison pour sa musique en l'isolant d'un vaste univers d'expressions musicales potentielles. Elle a même conditionné les musiciens à entendre que la musique en accord avec les harmoniques naturelles sonne faux.

En incorporant les instruments occidentaux à tons fixes dans la musique indienne, la puissance initiale et la pureté de cette musique a été déformée et polluée. On éloigne la musique de l'harmonie des lois de la nature, alors qu'elle est censée faire le contraire, nous amener plus en harmonie avec les lois de la nature. Nous pensons donc qu'il est important de sensibiliser le public à ce sujet.